查找算法的演化过程
查找算法的演化过程
顺序查找
字面意思,一个个节点查找判断,对数据条件没什么要求,最简单,也最慢。
/**
* 顺序查找
* @param arr 数组
* @param target 目标值
* @return 下标
*/
public static int getIndex(int[] arr, int target) {
// 记录比较多少次找到目标值
int index = 0;
for (int i = 0; i < arr.length; i++) {
index++;
if (arr[i] == target) {
System.out.println("顺序查找次数:" + index);
return i;
}
}
return -1;
}二分查找
如果我们能让数据有序,我们先找中间数,如果目标值大于中间数,则从中位数往后找,这一下子筛去一半的数据,如果刚好一样,则可以直接返回坐标。速度大幅提升。
/**
* 二分查找
* @param arr 数组
* @param target 目标值
* @return 下标
*/
public static int getIndexBinary(int[] arr, int target) {
int index = 0;
int left = 0;
int right = arr.length;
while (left < right) {
index++;
int mid = (left + right) >> 1;
int midVal = arr[mid];
if (midVal == target) {
System.out.println("二分查找次数:" + index);
return mid;
} else if (midVal > target) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return -1;
}插值查找
如果我的目标值很大,要查找的数组又很长,我知道目标值大概率是在数组的后面,但二分查找只能定位到中间位置,再往后筛选,能不能说我根据目标值的大小,推算出它的位置大概在哪里?如果不是再在剩下的范围找,比二分查找智能点儿。例如:我的数组存储从1到100,我要查询数组中是否有98这个数字。中间大概率是50左右,98肯定是在最后的区间内。
/**
* 插值查找
* @param arr 数组
* @param target 目标值
* @return 下标
*/
public static int interpolationSearch(int[] arr, int target) {
int index = 0;
int low = 0;
int high = arr.length - 1;
while (low <= high && target >= arr[low] && target <= arr[high]) {
index++;
// 与二分查找不同点在于中间点的确认 这里牵扯到了数学推理
int pos = low + (high - low) * (target - arr[low]) / (arr[high] - arr[low]);
if (arr[pos] == target) {
System.out.println("插值查找的次数:" + index);
return pos;
}
if (arr[pos] < target) {
low = pos + 1;
} else {
high = pos - 1;
}
}
return -1;
}二分优化查找
其实二分查找向左向右查找是不平衡的,也是说一边判断的次数要比另一边多,我们看图示例。

上图中第一行是所有的待查询的节点,然后不断二分查找,最后每个节点旁边灰色的数字就是找到该点时,判断过几次,下面是相应判断的代码。
while(low <= high)
{ //每步迭代可能都要做两次比较判断,有三个分支
int mid = (low + high) >> 1; //以中点为轴点
if(target < A[mid])
high = mid - 1; //深入前半段[low, mid-1]继续查找,这里只需要判断一次
else if(A[mid] < target)
low = mid + 1; //深入后半段[mid+1, high]继续查找,这里需要判断了两次
else
return mid; //在mid处命中
}
return -1; //查找失败,返回-1
} 可以看到如果不断向右查找,每次判断的次数都要比向左查找多一次判断。那能不能让向右向左都只判断一次。
/**
* 二分查找优化版本
* @param arr 数组
* @param target 目标值
* @return 下标
*/
public static int getIndexBinaryPlus(int[] arr, int target) {
int index = 0;
int low = 0;
int high = arr.length;
while (1 < high - low) {
index++;
int mid = (low + high) >> 1; //以中点为轴点,经比较后确定深入
if (target < arr[mid]) {
high = mid;
} else {
low = mid;
}
}
System.out.println("二分查找优化:"+index);
return (target == arr[low]) ? low : -1; //返回命中元素所在的位置或-1
} 我们再看一下查找的过程图:
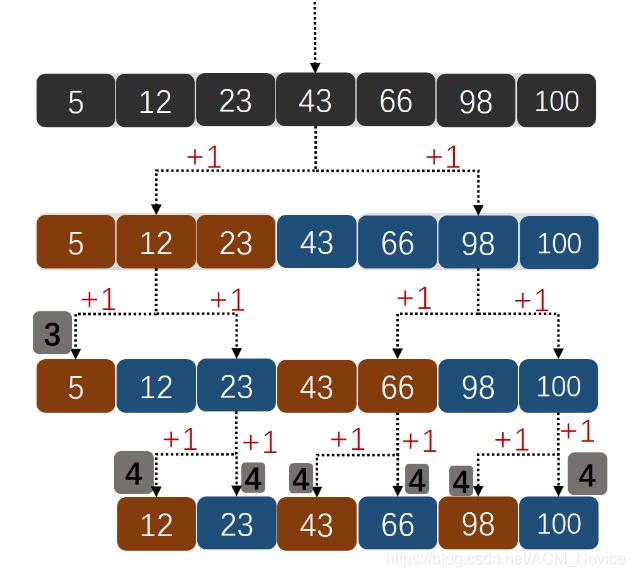
我们将之前二分查找比作方案A,现在版本比作方案B,我们可以看到对于最好情况,也就是中间数刚好是要找到数时,方案A可直接返回,方案B只能最后返回,但在方案B最好的情况下,要比方案A好,因为左右判断的次数是平衡的。
斐波那契查找
我在学习斐波那契查找算法时,一直不理解,为啥按照黄金分割点做定点效果会更好,其中看到的一篇文章说,因为标准二分查找,向左向右查找并不平衡,所以如果每次定点向右偏移一些,这样可以让整体处于均衡的状态。也就是说我每次都向右偏移一些,这样向右查询的次数就会减少,像左查询次数增加,这样动态的形成一种均衡。
/**
* 斐波那契查找
* @param arr 数组
* @param target 目标值
* @return 下标
*/
public static int fibonacciSearch(int[] arr, int target) {
int low = 0;
int high = arr.length - 1;
int k = 0;
int mid;
int f[] = fib();
// 找到扩容长度
while (high > f[k] - 1) {
k++;
}
// 扩容
int[] temp = Arrays.copyOf(arr, f[k]);
// 最后一位填充
for (int i = high + 1; i < temp.length; i++) {
temp[i] = arr[high];
}
while (low <= high) {
mid = low + f[k - 1] - 1;
if (target < temp[mid]) {
high = mid - 1;
k--;
} else if (target > temp[mid]) {
low = mid + 1;
k -= 2;
} else {
if (mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}索引查找
除了顺序查找,上面所有的查找算法的潜在条件就是数组有序,那如果数据本身无序,我们又想保证高性能的查询,我们可以为数据加上索引,每本书都有一个目录页,记录每个章节的页码,这样我想看具体的某一章,可以根据页码迅速定位。
但这样做又需要注意:
- 索引不能重复,这里牵扯到哈希碰撞的解决方案
- 相比原数据,我们需要维护一个索引数据,空间换时间思路
- 索引的更新
这里又有了不同的选择,顺序索引和哈希索引
其实数组中我们通过下标去直接访问数据,下标不就是一种索引嘛。我们可以顺着第一个下标,一直找到最大下标值所指的数据。
public void test() {
int[] arr = {1,2,3,4,5};
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
} 如果我们顺序的插入数据,第一个数插入index=0的位置,第二个数插入index=1的位置。那么可以理解下标index为顺序索引,它不仅指向实际的数据,索引与索引间存在顺序关系,arr[i-1] 在 arr[i] 之前插入。这样做的好处有什么呢?我们可以一次性找到某个索引后所有的数据,但是顺序索引的缺点就是我们需要顺序比较判断,就像顺序查找一样,不过可做二分优化。
这里我们可以想想Mysql中Innodb中使用B+树结构作为索引,该结构就有索引有序的特点。方便我们进行索引筛选的功能。
public void test() {
char[] arr = new char[5];
arr[0] = 'a';
arr[1] = 'b';
arr[2] = 'c';
arr[3] = 'd';
arr[4] = 'e';
} 还有一种实现是Hash索引,这里不对Hash计算深究,比方说第一个数,我们进行对Key进行Hash计算结果为1002,我们底层通过数组来实现存储,数组长度为5,则将1002余5,等于2,则我们不插入到0位置,而是直接插入到2位置,下一次可能插入4位置,这样索引与索引间不再存在顺序关系,但好处是,可以在常数时间内查找到对应的数据,
总结
每种算法都在原有算法的基础上对其进行一方面的优化,每种算法都有自己适用的范围,没有最好的,只有最合适的,这需要我们对每个算法的底层实现有着清晰的认识,从而根据具体的场景进行选择。

